어떤 글로 처음을 장식해야 할 지 고민이 많았습니다.
저는 고등학생이고, 아직 깨우치지 못 한 게 많지만 물리라는 학문에 대한 애정은 상당합니다.
아직 고등학교 물리1, 2도 제대로 안 뗀 애가 물리 블로그를 운영하니 어떤 분들께는 귀엽게 보일 수도 있겠죠.
나보다 똑똑한 사람들이 많은데 괜히 번데기 앞에서 주름잡는 꼴이 아닐까 싶긴 한데.
그냥, 겸손하고 온건하고 안전하게, 제가 아는 선에서 그냥 소소한 거 올리고,
예전에 궁금해했던 것들도 가끔 올리고,
힘들면 때로는 잠시 접어둘 수 있는 그런 작은 블로그나 하나 운영하는 것이 목적입니다.
각설하고, 주제로 돌아와서
제가 고등학교에 올라오고 나서 궁금해했던 것 중에
가장 기억에 남는 질문 하나로 첫 글을 시작해보려고 합니다.
두 물체의 속도 차가 c(=(빛의 속력)=약 300,000km/s)가 넘어요. 이게 가능한가요?
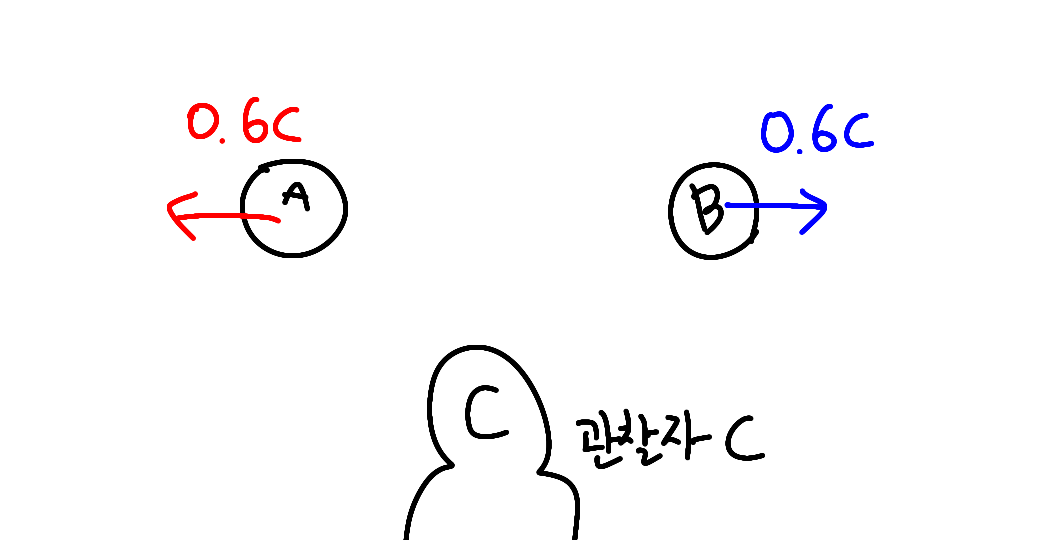
대충 예를 들어서,
물체 A가 왼쪽으로 0.6c, 물체 B가 오른쪽으로 0.6c로 일정하게 직선운동 한다고 할 때
상대속도를 구하는 공식에 따르면 두 물체 사이의 상대속도 크기가 1.2c가 되는데
이게 실제로 가능한 일인지를 묻고 싶은 것 같습니다.
왜냐하면 상대속도 공식은 이러하니까요.
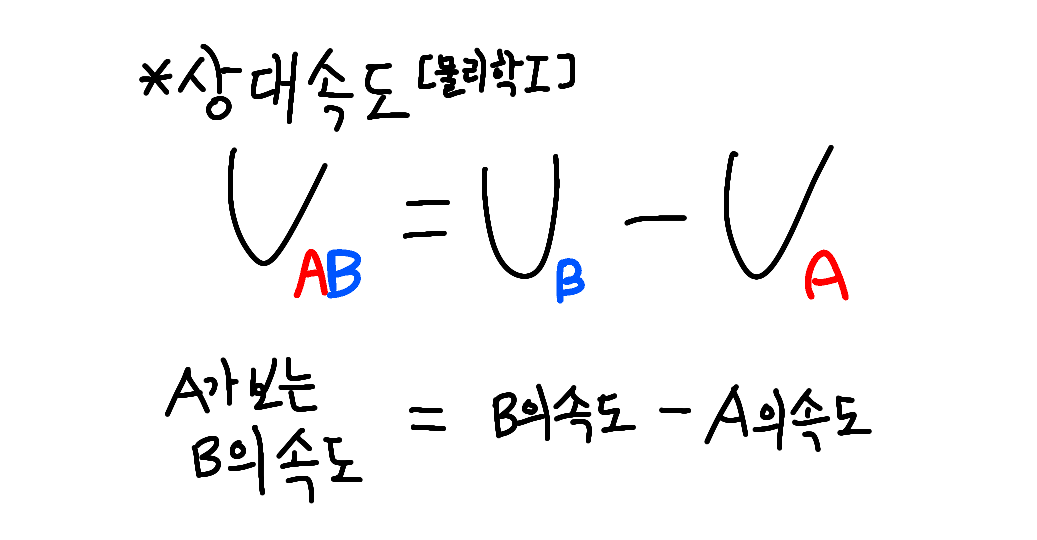
(가끔 좌변의 알파벳 AB의 위치를 바꿔쓰는 분들도 계시더군요. 일단 제가 배울 때 A가 보는 B의 속도는 AB로 쓴다고 배워서 그렇게 썼습니다.)
편의상 오른쪽을 (+)방향이라고 하겠습니다.
그러면 A가 보는 B의 속도는 +0.6c-(-0.6c)=+1.2c가 되겠죠.
B가 보는 A의 속도는 크기가 같고 부호가 반대.
그런데 상대성이론을 공부해본 학생들은 알겁니다.
모든 물체의 속도는 절대 빛의 속도 이상을 넘어설 수가 없다는 것을요.
모순이네요. 어디서부터 잘못됐을까요? 빛의 속도를 넘어서는 경우도 있는 걸까요?
잘못된 부분은 상대속도를 구하는 식에 있습니다.
사실 1.2c로 못 갑니다.
상대속도가 c를 넘어설 수가 없다는 얘기입니다.
속도가 너무 빠를 때 그냥 고전역학 스타일대로 물리량을 구해버리면 원하는 값을 도출하는 걸 기대하기는 힘들 겁니다.
우리가 흔히 알고 있는 상대속도 식은 사실 근사값이고,
정확하고 엄밀하게 속도를 구하려고 한다면 아래 식의 도움을 받아야 합니다.
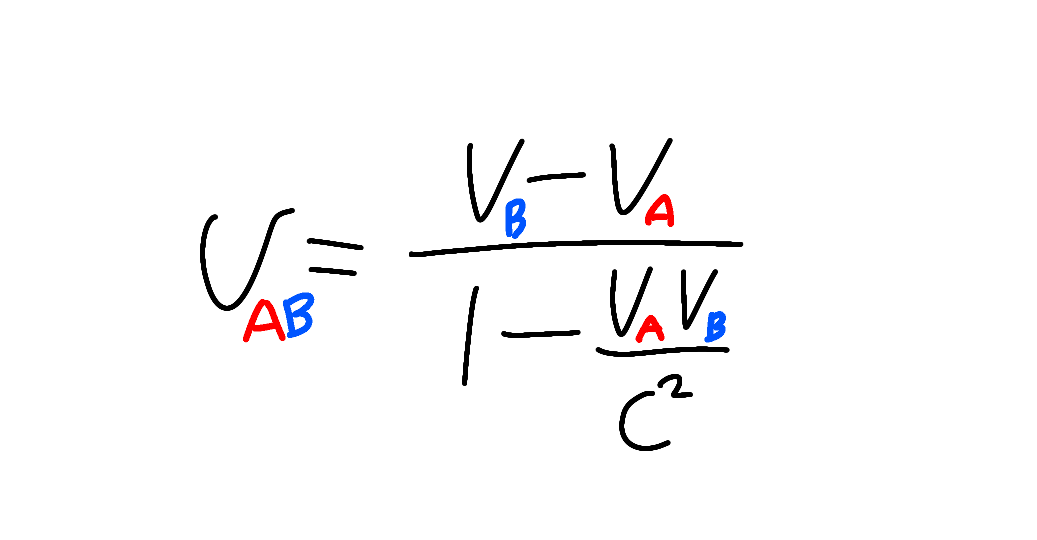
분모에 자질구레한 것들이 추가됐죠.
여기서 c는 빛의 속도를 가리킵니다.
지금까지 저희가 알고 있던 상대속도 식은 갈릴레이변환을 이용한 공식인데,
위 식은 로렌츠변환을 이용해 유도한 상대론적 상대속도 공식입니다.
이 글을 올리기 위해서 자료를 이것저것 찾아보다가 식의 유도과정도 함께 올릴까 했었는데,
첫 글치고는 너무 무겁게 들어가는 감이 있지 않나 싶기도 하고, 제가 이걸 받아들이는 데도 시간이 오래 걸려서... 정리하고 올리기까지 하려면 시간이 꽤 걸릴 것 같았습니다.
그래서 나중에 기회가 되면 상대론적 상대속도 공식 유도과정도 따로 올려보려고 합니다.
아무튼 위 식을 이용해서 예시에서의 상대속도를 구한다고 하면 아래와 같이 구할 수 있을 것입니다.
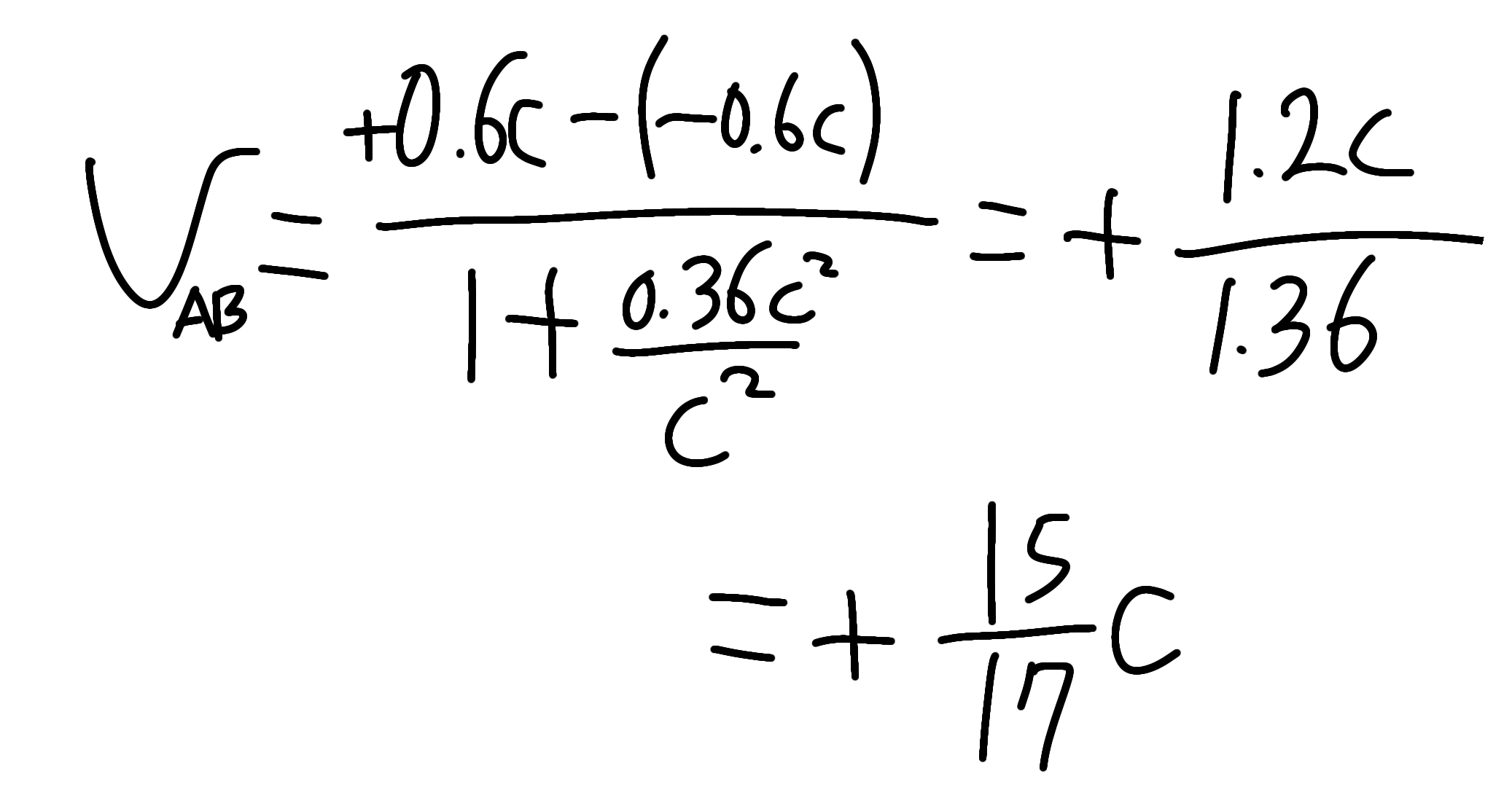
엄연한 식은 저렇게 복잡함에도 불구하고
처음에 상대속도를 굳이 v=v1-v2 이렇게 배우는 이유는 그때 배우는 역학체계에서는 v1과 v2의 크기가 너무 작아
분모의 1-v1v2/c^2가 결국 1에 가까운 숫자가 되기 때문입니다.
c에 비하면 v1과 v2는 너무 작아요. 무시하는 것이 낫죠.
애초에 고전역학에서의 물리량을 따져본다고 하면 갈릴레이 변환을 쓰는 게 나아요.
철수와 영희가 미쳤다고 초속 십만킬로로 달리고 그러진 않죠.
얘네 요즘 하이탑에서 하는 짓거리 보면 가관이긴 하던데
제가 오늘 준비한 내용은 여기까지입니다.
이 질문을 해결하기 위해서 학교 선생님이나 책, 인터넷 등 많은 도움을 받았는데,
제가 도움을 받았던 것처럼 다른 사람들에게도 이 글이 도움이 되었으면 합니다.
앞서 말씀드렸듯이 상대론적 상대속도 유도과정은 추후에 올려보도록 하겠습니다.
혹시라도 제 글에 오류나 오개념이 포함되어있다면 댓글로 따끔하게 지적해주시면 좋겠습니다.
아무쪼록 부족한 글 봐주셔서 감사합니다.